THE MOST PRECIOUS THING FOR ALL PEOPLE IS ART AND LIVING FROM IT. BECAUSE EVERYTHING ELSE, WAR, CHANGES, DESTROY THEM, WHILE ART IS ALWAYS SAVED /HIPPARHOS

 

Born	c. 190 BC Nicaea, Kingdom of Bithynia (modern-day İznik, Bursa, Turkey)
Died	c. 120 BC (around age 70) Rhodos Greece
Occupations	AstronomerMathematicianGeographer

Hipparchus (/hɪˈpɑːrkəs/; Greek: Ἵππαρχος, Hipparkhos; c. 190 – c. 120 BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hipparchus was born in Nicaea, Bithynia, and probably died on the island of Rhodes, Greece. He is known to have been a working astronomer between 162 and 127 BC.

Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by Meton of Athens (fifth century BC), Timocharis, Aristyllus, Aristarchus of Samos, and Eratosthenes, among others.

He developed trigonometry and constructed trigonometric tables, and he solved several problems of spherical trigonometry. With his solar and lunar theories and his trigonometry, he may have been the first to develop a reliable method to predict solar eclipses.

His other reputed achievements include the discovery and measurement of Earth’s precession, the compilation of the first known comprehensive star catalog from the western world, and possibly the invention of the astrolabe, as well as of the armillary sphere that he may have used in creating the star catalogue. Hipparchus is sometimes called the “father of astronomy”, a title conferred on him by Jean Baptiste Joseph Delambre in 1817^]

Life and work

Hipparchus was born in Nicaea (Greek: Νίκαια), in Bithynia. The exact dates of his life are not known, but Ptolemy attributes astronomical observations to him in the period from 147 to 127 BC, and some of these are stated as made in Rhodes; earlier observations since 162 BC might also have been made by him. His birth date (c. 190 BC) was calculated by Delambre based on clues in his work. Hipparchus must have lived some time after 127 BC because he analyzed and published his observations from that year.

In the second and third centuries, coins were made in his honour in Bithynia that bear his name and show him with a globe.

Relatively little of Hipparchus’s direct work survives into modern times. Although he wrote at least fourteen books, only his commentary on the popular astronomical poem by Aratos was preserved by later copyists. Most of what is known about Hipparchus comes from Strabo‘s Geography and Pliny‘s Natural History in the first century; Ptolemy’s second-century Almagest; and additional references to him in the fourth century by Pappus and Theon of Alexandria in their commentaries on the Almagest.

Hipparchus’s only preserved work is Commentary on the Phaenomena of Eudoxus and Aratus (Greek: Τῶν Ἀράτου καὶ Εὐδόξου φαινομένων ἐξήγησις). This is a highly critical commentary in the form of two books on a popular poem by Aratus based on the work by Eudoxos.^[Hipparchus also made a list of his major works that apparently mentioned about fourteen books, but which is only known from references by later authors. His famous star catalog was incorporated into the one by Ptolemy and may be almost perfectly reconstructed by subtraction of two and two-thirds degrees from the longitudes of Ptolemy’s stars. The first trigonometric table was apparently compiled by Hipparchus, who is consequently now known as “the father of Trigonometry

 Eudoxus in the 4th century BC and Timocharis and Aristillus in the 3rd century BC already divided the ecliptic in 360 parts (our degrees, Greek: moira) of 60 arcminutes and Hipparchus continued this tradition. It was only in Hipparchus’s time (2nd century BC) when this division was introduced (probably by Hipparchus’s contemporary Hypsikles) for all circles in mathematics. Eratosthenes (3rd century BC), in contrast, used a simpler sexagesimal system dividing a circle into 60 parts. Hipparchus also adopted the Aristarhus astronomical Greek πῆχυς pēchys) that was equivalent to 2° or 2.5° (‘large cubit’).

Hipparchus’s long draconitic lunar period (5,458 months = 5,923 is post-Hipparchus so the direction of transmission is not settled by the tablets.

Geometric construction used by Hipparchus in his determination of the distances to the Sun and Moon

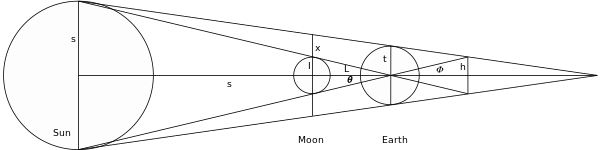
Geometry, trigonometry and other mathematical techniques

Hipparchus was recognized as the first mathematician known to have possessed a trigonometric table, which he needed when computing the eccentricity of the orbits of the Moon and Sun. He tabulated values for the chord function, which for a central angle in a circle gives the length of the straight line segment between the points where the angle intersects the circle. He may have computed this for a circle with a circumference of 21,600 units and a radius (rounded) of 3,438 units; this circle has a unit length for each arcminute along its perimeter. (This was “proven” by Toomer, but he later “cast doubt“ upon his earlier affirmation^. Other authors have argued that a circle of radius 3,600 units may instead have been used by Hipparchus.) He tabulated the chords for angles with increments of 7.5°. In modern terms, the chord subtended by a central angle in a circle of given radius R equals R times twice the sine of half of the angle, i.e.:chord⁡�=2�⋅sin⁡12�The now-lost work in which Hipparchus is said to have developed his chord table, is called Tōn en kuklōi eutheiōn (Of Lines Inside a Circle) in Theon of Alexandria‘s fourth-century commentary on section I.10 Trigonometry was a significant innovation, because it allowed Greek astronomers to solve any triangle, and made it possible to make quantitative astronomical models and predictions using their preferred geometric techniques.

Hipparchus must have used a better approximation for π than the one given by Archimedes of between 3+¹⁰⁄₇₁ (≈ 3.1408) and 3+¹⁄₇ (≈ 3.1429). Perhaps he had the approximation later used by Ptolemy, sexagesimal 3;08,30 (≈ 3.1417) (Almagest VI.7).

Hipparchus could have constructed his chord table using the Pythagorean theorem and a theorem known to Archimedes.

The stereographic projection was ambiguously attributed to Hipparchus by Synesios (c. 400 AD), and on that basis Hipparchus is often credited with inventing it or at least knowing of it. However, some scholars believe this conclusion to be unjustified by available evidence.The oldest extant description of the stereographic projection is found in Ptolemy‘s Planisphere (2nd century AD)

There are several indications that Hipparchus knew spherical trigonometry, but the first surviving text discussing it is by Menelaus of Alexandria in the first century, who now, on that basis, commonly is credited with its discovery. (Previous to the finding of the proofs of Menelaus a century ago, Ptolemy was credited with the invention of spherical trigonometry.) Ptolemy later used spherical trigonometry to compute things such as the rising and setting points of the ecliptic, or to take account of the lunar parallax. If he did not use spherical trigonometry, Hipparchus may have used a globe for these tasks, reading values off coordinate grids drawn on it, or he may have made approximations from planar geometry, or perhaps used arithmetical approximations developed by Pythagoras