****************T H A L E S

THALES of Miletus was a Greek mathematician who lived 2600 years ago. He formulated a theorem with the following meaning: Every triangle inscribed in a circle has a right angle if one of the sides of the triangle is the diameter of the circle. One easy way to construct a right-angled triangle, is to use Thales’ theorem. Thales theorem states that if one of the sides of a triangle is along the diameter of a circle, and if the third vertex also lies on the circle, then the angle at the third vertex is a right angle.The triangle A B C is inscribed in a circle in such a way.

The Pythagorean theorem
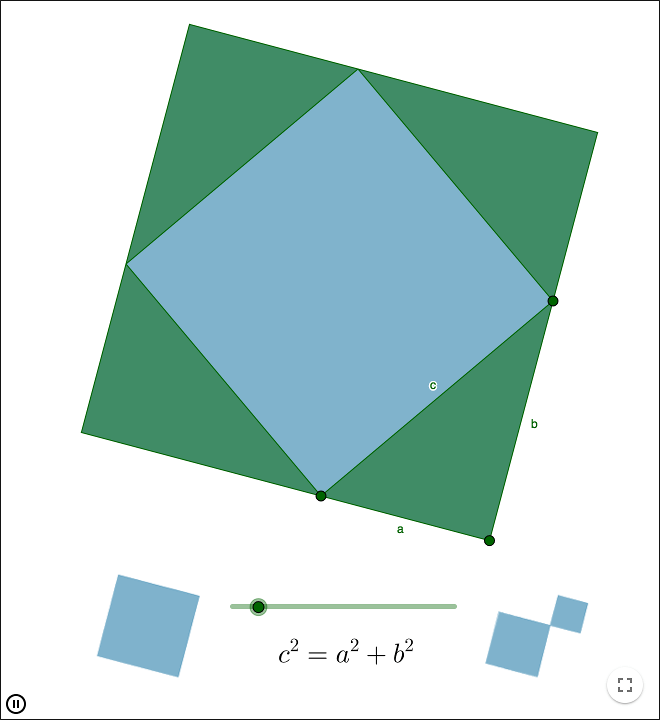
For a right-angled triangle with shorter sides a and b, and the hypotenuse c, following holds:
c2=a2+b2�2=�2+�2
Conversely, if three positive numbers a, b, c satisfy c2=a2+b2�2=�2+�2; then the numbers can be the lengths of the sides of a right-angled triangle.
There are many proofs of the Pythagorean theorem that are based on interpreting the square of a number as the area of a square. You then prove that the area of the two smaller squares in the image below, have the same total area as the large square.
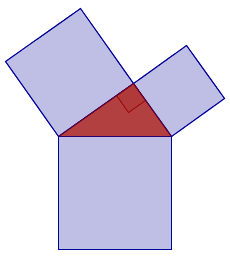
One of the easiest proofs is shown in the worksheet above. A more difficult proof where the smaller squares are cut and then put together as a larger square is shown below.
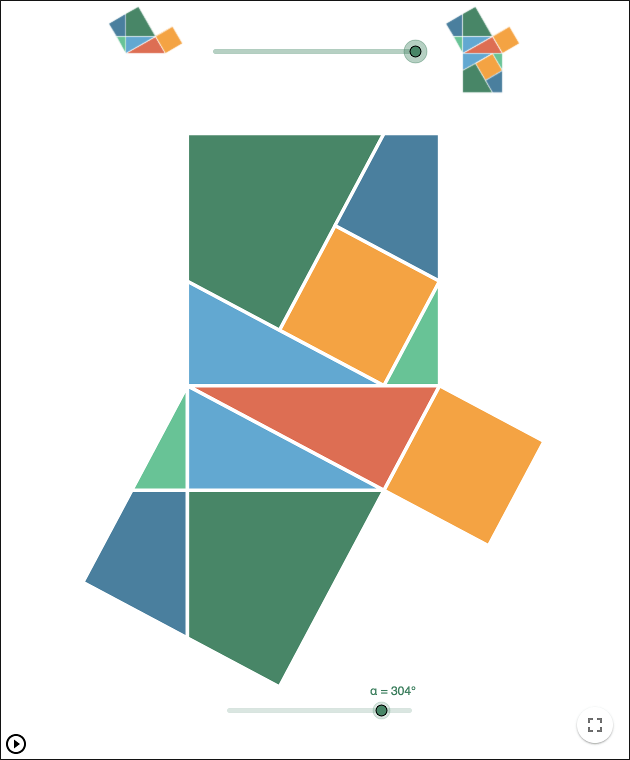
Exercise 1
Use the picture above to prove Thales’ theorem!
Dynamic Pythagoras’ tree
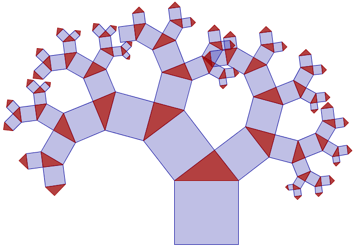
By using Thales theorem, it is possible to make a dynamic variant of a fractal called Pythagoras tree.
EXERCISE 2
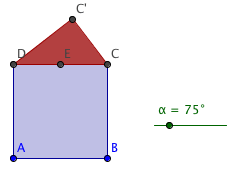
- Input two points A� and B� and a slider α� representing an angle. Use the tool Regular Polygon to make a square as in the picture above.
- Use the tool Midpoint or Centre to make the midpoint E� between C� and D�. Use the tool Rotate, to rotate C� around E� by the angle α�. Move the slider to see the point C′�′ move. Make a triangle as in the picture above. The triangle will be a right-angled triangle due to Thales’ theorem.
- Pick Tools -> Create New Tool. Make a tool that has the objects C�, C′�′, D�, and the two polygons as output objects. The tool will have A�, B�, and α� as input objects.
- Build a tree by using the tool. Start by clicking two points, then enter
αin the input box that shows up.
You can make variations of Pythagoras’ tree. For some examples see Variations on Pythagoras’ Tree.

Much of our modern science, and astronomy in particular, has roots in the ancient world. In particular, the Greek philosophers studied the cosmos and tried to use the language of mathematics to explain everything. The Greek philosopher Thales was one such man. He was born around 624 BCE,from (Miletus was a Greek island in Ionia Asia Minor, now modern Turkey) and he came from a distinguished family.
It is difficult to write about Thales since none of his own writing survives. He was known to be a prolific writer, but as with so many documents from the ancient world, his vanished through the ages. He is mentioned in other people’s works and seems to have been quite well-known for his time among fellow philosophers and writers. Thales was an engineer, scientist, mathematician, and philosopher interested in nature. He may have been the teacher of Anaximander (611 BC – 545 BCE), another philosopher.
Some researchers think Thales wrote a book on navigation, but there is little evidence of such a tome. In fact, if he wrote any works at all, they did not even survive until the time of Aristotle (384 BCE- 322 BCE). Even though the existence of his book is debatable, it turns out that Thales probably did define the constellation Ursa Minor.
Despite the fact that much of what is known about Thales is mostly hearsay, he was definitely well-respected in ancient Greece. He was the only philosopher before Socrates to be counted among the Seven Sages. These were philosophers in the 6th century BCE who were statesmen and law-givers, and in Thales’s case, a natural philosopher (scientist).
There are reports that Thales predicted an eclipse of the Sun in 585 BCE. While the 19-year cycle for lunar eclipses was well known by this time, solar eclipses were harder to predict, since they were visible from different locations on Earth and people were not aware of the orbital motions of the Sun, Moon, and Earth that contributed to solar eclipses. Most likely, if he did make such a prediction, it was a lucky guess based on experience saying that another eclipse was due.
After the eclipse on 28 May, 585 BCE, Herodotus wrote, “Day was all of a sudden changed into night. This event had been foretold by Thales, the Milesian, who forewarned the Ionians of it, fixing for it the very year in which it took place. The Medes and Lydians, when they observed the change, ceased fighting, and were alike anxious to have terms of peace agreed on.”
Impressive but Human
Thales is often credited with some impressive work with geometry. It is said he determined the heights of pyramids by measuring their shadows and could deduce the distances of ships from a vantage point onshore.
How much of our knowledge of Thales is accurate is anyone’s guess. Most of what we know is due to Aristotle who wrote in his Metaphysics: “Thales of Miletus taught that ‘all things are water’.” Apparently Thales believed the Earth floated in water and everything came from water.
Like the absent-minded professor stereotype still popular today, Thales has been described in both glowing and derogatory tales. One story, told by Aristotle, says Thales used his skills to predict that the next season’s olive crop would be bountiful. He then purchased all the olive presses and made a fortune when the prediction came true. Plato, on the other hand, told a story of how one night Thales was gazing at the sky as he walked and fell into a ditch. There was a pretty servant girl nearby who came to his rescue, who then said to him “How do you expect to understand what is going on up in the sky if you do not even see what is at your feet?”
Thales died about 547 BCE in his home of Miletus.
Edited and updated by Carolyn Collins Petersen.
This entry was posted in schönros by Konstantin. Bookmark the permalink.Edit
